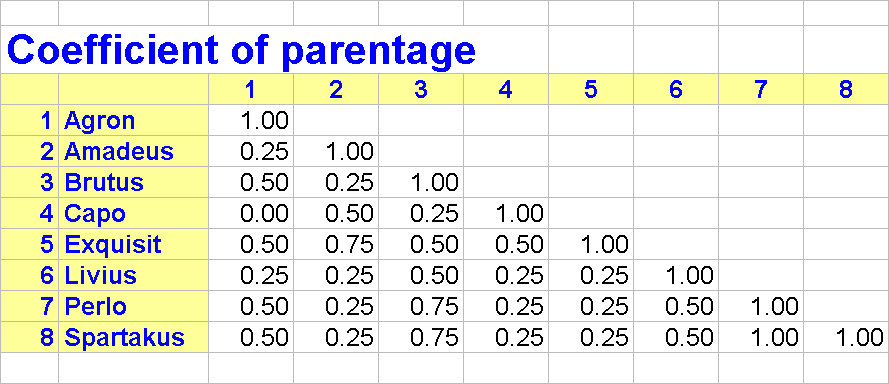
Beispiel: cop-Werte zwischen Österreichischen Qualitätsweizensorten
aufgrund ihrer Pedigrees (vereinfachte Berechnung bis zu Großeltern)
BESCHREIBUNG GENETISCHER DIVERSITÄT
1. Bestimmung genetischer
Ähnlichkeit / Distanz
1.1. Phänotypische
Ähnlichkeit
1.2. Verwandtschaft
(Pedigree, coefficient of parentage)
1.3. Molekulare
genetische Marker
2. Darstellungsmethoden
2.1. Genetische
Distanz
2.2. Clusteranalyse
/ Dendrogramm
2.3. Multidimensional
Scaling (MDS)
LITERATUR
BESCHREIBUNG GENETISCHER DIVERSITÄT
Neben der direkten Selektion von Genotypen haben auch die Bestimmung
der genetischen Distanz zwischen einzelnen Genotypen und die Beschreibung
der genetischen Diversität in Populationen insgesamt eine große
Bedeutung für die Züchtung. Damit ist es möglich, die Vielzahl
der in Zuchtprogrammen vorhandenen Genotypen zu gruppieren und überschaubar
zu strukturieren. Aufgrund derartiger Strukturierungen kann z.B. die Auswahl
von Kreuzungseltern erfolgen.
1. Bestimmung genetischer Ähnlichkeit / Distanz
Die genetische Distanz ist ein Maß für Ähnlichkeit oder Verwandtschaft zwischen Genotypen. Distanz und Ähnlichkeit werden oft wechselweise verwendet (Distanz = 1 – Ähnlichkeit), Distanz ist sozusagen das Gegenteil der Ähnlichkeit.
1.1. Phänotypische Ähnlichkeit
Zunächst kann genetische Distanz einfach phänotypisch ausgedrückt
werden. Mit Hilfe von standardisierten Merkmalswerten kann damit eindimensional
oder multidimensional eine Distanz zwischen Genotypen berechnet werden.
Diese spiegelt nur ungefähr die genetischen Verhältnisse wieder,
hängt dagegen u.U. stark von den Umweltverhältnissen ab, welche
die phänotypischen Meßwerte modifizieren können.
1.2. Verwandtschaft (Pedigree, coefficient of parentage = cop)
Aufgrund der Verwandtschaftsverhältnisse von Genotypen (z.B. Schwesterlinien
mit einem oder mehreren gemeinsamen Eltern oder Großeltern usw.)
kann die genetische Distanz genauer erfaßt werden. Dabei wird ein
sog. coefficient of parentage (cop, "Elternschaftskoeffizient")
zwischen 2 Sorten aufgrund ihrer jeweiligen Stammbäume errechnet.
Diese Berechnung basiert auf folgenden Annahmen:
1. Eine Sorte aus einer bestimmten Kreuzung erhält jeweils die
Hälfte der Gene von den beiden Eltern.
2. Zwei Sorten, die einen gemeinsamen Elter aufweisen, haben also rein
statistisch an 50 % der Genorte die gleichen Allele, also cop=0.5. Zwei
Sorten mit einem gemeinsamen Großelter haben 25 % der Genloci gemeinsam,
also cop=0.25. Dagegen haben zwei Sorten ohne gemeinsame Vorfahren einen
cop von 0.
3. Für eine direkte Selektion aus einer Sorte wird ein cop von
0.75 angenommen.
4. Weiters wird vorausgesetzt, daß alle Vorfahren nicht miteinander
verwandt und alle Sorten, Vorfahren bzw. Elternlinien homozygot und homogen
sind.
Die Genauigkeit der so ermittelten cop-Werte (diese sind Wahrscheinlichkeitswerte)
erfährt jedoch eine wesentliche Einschränkung, die auf die Selektion
innerhalb der Kreuzung zurückzuführen ist, wodurch oft die Allele
eines der beiden Eltern bevorzugt selektiert werden. Auch genetische Drift
und unbekannte (nicht berücksichtigte) Verwandtschaftsverhältnisse
zwischen Eltern führen dazu, daß der errechnete cop-Wert von
der tatsächlichen genetischen Distanz mehr oder weniger stark abweicht.

1.3. Molekulare genetische Marker
Molekulare Marker (Proteinmarker oder DNA-Marker) zur Bestimmung der
genetischen Distanz haben gegenüber den phänotypischen Markern
zunächst einmal den Vorteil, daß sie unabhängig von Umwelteinflüssen
sind. Weiters beschreiben molekulare Marker die tatsächlichen Verhältnisse
auf bestimmten Genloci und nicht bloß wahrscheinliche Verhältnisse,
wie dies in der Berechnung der cop-Werte geschieht. Im Gegensatz zu cop-Werten
sind auch keine Stammbauminformationen erforderlich, die u.U. unvollständig
oder falsch sein können.
Wenn molekulare Marker in genügender Dichte vorhanden sind, ist
ein Großteil des Genoms darstellbar, womit die Schätzung der
Distanz zwischen Genotypen sehr genau wird. Zur Berechnung der genetischen
Distanz wird für jeden Marker das Vorhandensein bestimmter Banden
tabellarisch binär (1 und 0, Bande ist vorhanden oder abwesend) dargestellt,
sodann werden alle paarweisen Distanzen zwischen Genotypen aufgrund bestimmter
Distanzmaße
(unterschiedlich je nach Markertyp, z.B. "Nei & Li") ermittelt.
2. Darstellungsmethoden
2.1. Genetische Distanz
Die genetische Distanz ist am einfachsten tabellarisch (als Distanzmatrix)
darstellbar, jedoch werden solche Tabellen rasch unübersichtlich und
unbrauchbar, wenn die Anzahl der Genotypen höher wird. Ein Sortiment
von 60 Sorten führt bereits zu einer Anzahl von 1770 paarweisen Distanzen
und damit zu einer sehr großen Tabelle.
2.2. Clusteranalyse / Dendrogramm
Mit Hilfe von Clusteranalysen ist es ganz allgemein möglich, eine
Vielzahl von ungeordneten Objekten aufgrund von Ähnlichkeit und sachlicher
Verwandtschaft in kleine, homogene Gruppen zu zerlegen und somit zu klassifizieren.
Dabei wird zwischen den zu beurteilenden Objekten, die in ihren Merkmalen
mit Hilfe einer Datenmatrix beschrieben werden, zunächst nach bestimmten
Algorithmen paarweise die Ähnlichkeit dieser Objekte gemessen, danach
werden in einem zweiten Schritt mit Hilfe dieser Ähnlichkeiten Gruppen
gebildet, wobei der Abstand zwischen Objekten innerhalb einer Gruppe stets
kleiner ist als zwischen den Gruppen. "Ähnliche Objekte" sind folglich
solche, die nach Berücksichtigung aller ihrer Merkmale in der gleichen
Gruppe zusammengefaßt werden, "unähnliche Objekte" gehören
verschiedenen Gruppen an. Ergebnisse von Clusteranalysen werden meist
als Dendrogramme ("Baumdiagramme") dargestellt.
Die Anwendung der Clusteranalyse in der Pflanzenzüchtung ist etwa
in der Kreuzungszüchtung sinnvoll, wenn es gilt, genotypisch möglichst
unterschiedliche Kreuzungseltern zu finden, um in deren Nachkommenschaften
eine starke Aufspaltung zu erreichen; auch bei der Selektion in Linienpopulationen,
wo für eine große Anzahl von Linien viele Einzelbeobachtungen
in der Selektionsentscheidung Berücksichtigung finden sollen, oder
im Rahmen der Evaluierung von Genbankherkünften kann mit einer Clusteranalyse
das Material auf überschaubare Gruppen eingeengt und damit eine Vorselektion
durchgeführt werden.
In letzter Zeit werden Clusteranalysen häufig verwendet, um Genotypen
mittels molekulargenetischer Marker wie RFLPs, RAPDs od. SSRs (Mikrosatelliten)
nach deren genetischer Distanz zu gliedern (z.B. UPGMA-Methode).
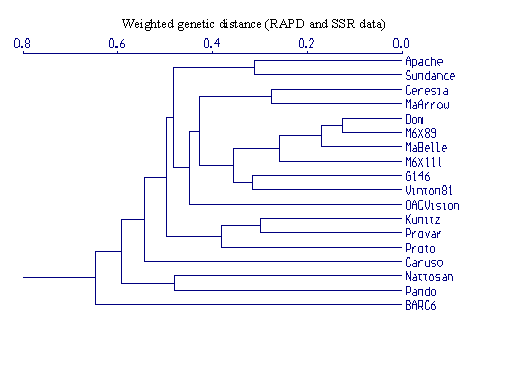

Beispiel 2: Dendrogramm von 60 Weizensorten
aus Ungarn, Österreich und Deutschland nach Bestimmung der genetischen
Distanz mittels eines Mikrosatellitensets (UPGMA clustering of SSR (Nei
and Li) data; aus: Stachel et al., 2000)
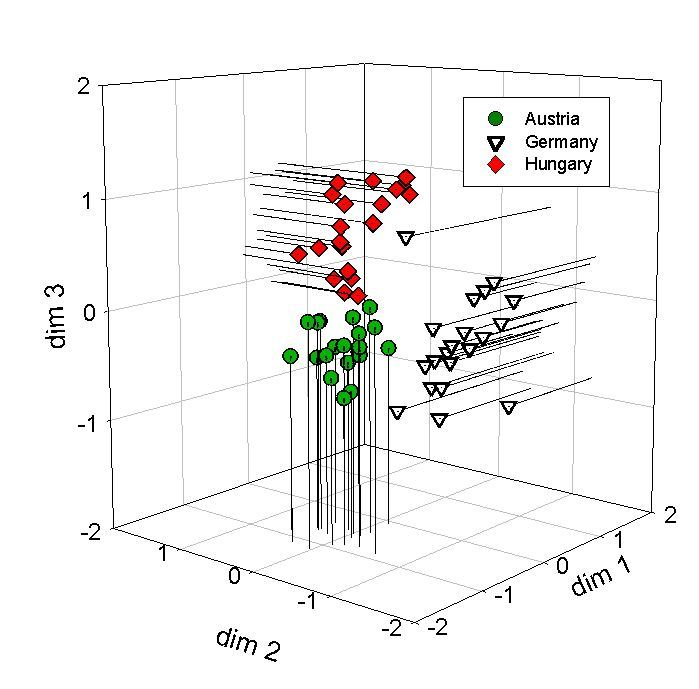
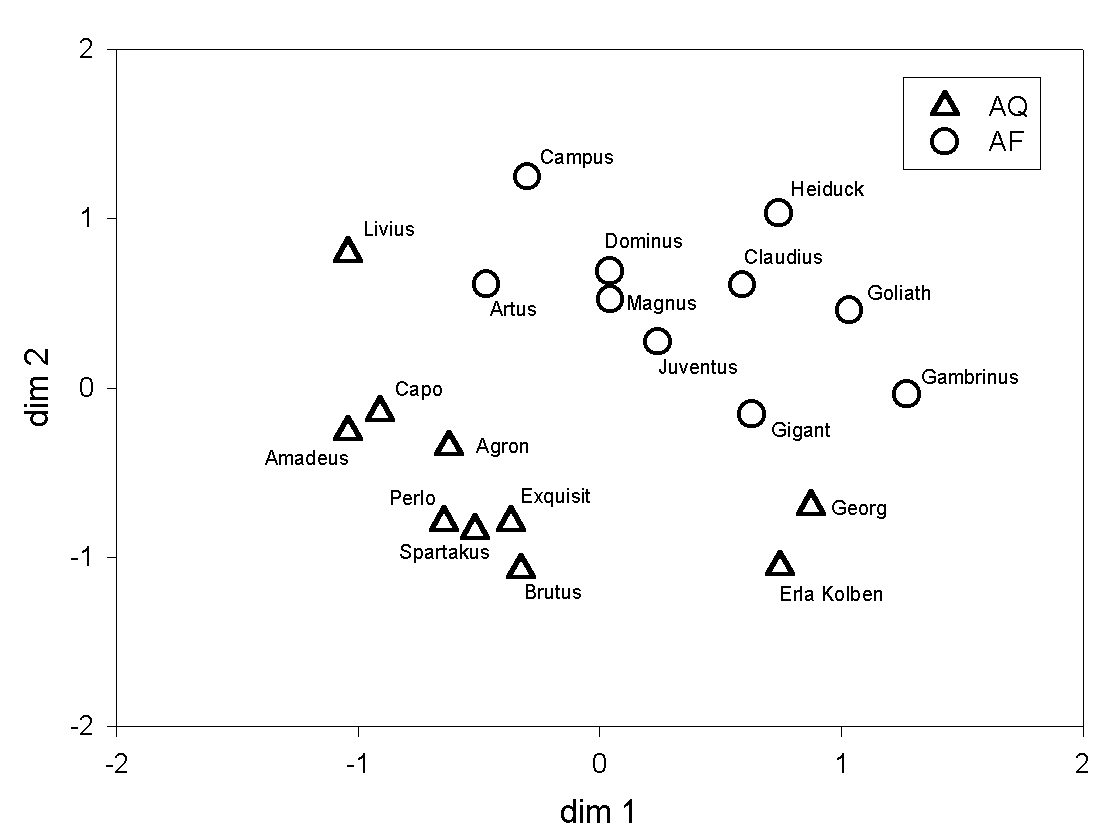
2.3. Multidimensional Scaling (MDS)
MDS ist eine multivariate Methode zur Darstellung der Ähnlichkeit/Unähnlichkeit
von beobachteten Objekten (z.B. Genotypen) in einem n-dimensionalen, euklidischen
Raum (z.B. n=2 oder 3), wobei die Abstände zw. den Objekten so gut
als möglich den beobachteten Abständen in einer Distanzmatrix
entsprechen sollen.
Prinzip: Von einer Distanzmatrix oder Anfangskonfiguration ausgehend
wird iterativ eine monotone Funktion für vorgegebene n Dimensionen
angepaßt (ähnlich wie z.B. bei Principal Component Analysis
PCA), bis ein Konvergenzkriterium erreicht ist. Die Qualität der Anpassung
wird mittels einer eigenen Statistik (stress) überprüft; je geringer
der "STRESS", desto besser die Anpassung.
Vorteile gegenüber der Clusteranalyse:
Die genetische Distanz ist bei MDS zwischen allen Einzelobjekten sichtbar
und nicht nur zwischen wenigen einzelnen, bevor diese in der hierarchischen
Clusteranalyse im Dendrogramm zu einer Gruppe verschmelzen.
Vorteile gegenüber Principal Components:
Ergebnisse von MDS sind denen der PCA ähnlich. Jedoch werden die
kleineren Abstände zwischen Punkten durch MDS wesentlich besser wiedergegeben
als durch PCA. In PCA sind die erste, zweite, dritte usw. Komponente abnehmend
nützlich für die Erklärung der Gesamtvariation, in MDS sind
alle Dimensionen gleich wertvoll, weshalb genetische Distanzen wirklichkeitsgetreuer
und weniger verzerrt wiedergegeben werden können.
DOLDI, M.-L., J. VOLLMANN & T. LELLEY, 1997, Genetic
diversity in soybean as determined by RAPD and microsatellie analysis,
Plant Breeding 116: 331-335.
KARP, A., P. G. ISAAC & D. S. INGRAM, 1998, Molecular
tools for screening biodiversity, Chapman & Hall, London.
LEBEDA, A. & T. JENDRULEK, 1987, Cluster analysis
as a method for evaluation of genetic similarity in specific host - parasite
interaction (Lactuca sativa - Bremia lactucae), Theor. Appl. Genet. 75:194-199.
NEI, M. & W. H. LI, 1979, Mathematical model
for studying genetic variation in terms of restriction endonucleases, Proc.
Natl. Acad. Sci. USA 76:5269-5273.
RUCKENBAUER, P., 1976, Cluster-Analysen und ihre Möglichkeiten
zur Erfassung von Komplexeigenschaften in der Getreidezüchtung, Arbeitstagung,
Arbeitsgemeinschaft Saatzucht-leiter Gumpenstein, 157-168.
STACHEL, M., T. LELLEY, H. GRAUSGRUBER & J. VOLLMANN,
2000, Application of microsatellites in wheat (Triticum aestivum
L.) for studying genetic differentiation caused by selection for different
adaptation and use, Theor. Appl. Genet. 100: 242-248.
VERONESI, F. & M. FALCINELLI, 1988, Evaluation of
an Italian germplasm collection of Festuca arundinacea Schreb. through
a multivariate analysis, Euphytica 38:211-220.
Siehe auch: "Selektion"